Les réseaux de neurones

Introduction

Machine learning : limites et conséquences

Le machine learning, apprentissage automatique ou apprentissage statistique en français, est une technologie d’intelligence artificielle basée sur le fait que la machine peut apprendre toute seule en se basant sur des modèles statistiques permettant d’effectuer des analyses prédictives. Cependant, cette méthode d’apprentissage requiert que ces données qui lui sert d’exemples soient, au préalable, triées par un expert humain pour ne laisser que les caractéristiques nécessaires à l’apprentissage (extraction de caractéristiques). Mais, dès que ces caractéristiques deviennent trop nombreuses, cette extraction devient quasi-impossible. Et c’est là qu’intervient les réseaux de neurones (réseaux de neurones artificiel).

Réseau de neurones artificiel

Un réseau de neurones artificiels ou Neural Network est un système informatique s’inspirant du fonctionnement du cerveau humain pour apprendre. C'est une association, en un graphe plus ou moins complexe, d’objets élémentaires : des neurones formels. Les principaux réseaux se distinguent par l’organisation du graphe (en couches, complets. . . ).

Les réseaux de neurones sont largement utilisés surtout dans le domaine de la reconnaissance d’image, de voix, de détection de cancer, etc. Il existe plusieurs types de réseaux de neurones, plutôt dire plusieurs architectures de réseaux de neurones. Parmi eux, on trouve les réseaux de neurones récurrents(RNN) appelé aussi les réseaux Feed-back, les réseaux de neurones autoorganisés, les réseaux de neurones Feed forward (propagation avant), etc. Dans le cadre de ce rapport nous allons nous concentrer sur les réseaux de neurones du type Feed Forward et plus précisément sur les perceptrons multicouches.

Dans le contexte de la classification d’images, balancer des images brutes sur un réseau de neurones permettra à ces réseaux de trouver les caractéristiques de ces images et enfin pouvoir faire des prédictions sur d’autres images qu’il n’a jamais encore vu. Cependant, les réseaux de neurones communément appelé perceptron multicouches (MLP) auront des difficultés à reconnaitre de grandes images. Ceci est dû à cause de la croissance exponentielle du nombre de connexions avec la taille de l'image et du fait que chaque neurone est « totalement connecté » à chacun des neurones de la couche précédente et suivante. Les MLPs auront aussi de difficulté à reconnaitre un objet qui est placé dans une autre position, angle différente par rapport aux images utilisés pendant l’entrainement. Et c’est ce qui fait intervenir les réseaux de neurones convolutifs (CNN pour Convolutional Neural Network) pour résoudre ces genres de problèmes.

Les CNN

Les réseaux de neurones convolutifs désignent une sous-catégorie de réseaux de neurones: ils présentent en effet toutes les caractéristiques des MLPs. Cependant, les CNN sont spécialement conçus pour traiter des images en entrée. Et apportent de nouvelles fonctionnalités dans le traitement d’images.

Neurone artificiel (Perceptron)

Le perceptron

Le perceptron aussi communément appelé neurone artificiel ou neurone formel, est un algorithme d’apprentissage automatique supervisé de classification binaire. Il s’agit du type de réseau de neurones artificiels le plus simple. Les perceptrons, ont été créés par Frank Rosenblatt en 1958. Son créateur l’a comparé à des neurones capables de répondre à des stimuli externes d’une manière qui imite les vrais neurones biologiques dans sa publication The perceptron : a probabilistic model for information storage and organization in the brain.

Le perceptron est un classifieur linéaire. Ce type de réseau neuronal ne contient aucun cycle (il s'agit d'un réseau de neurones à propagation avant). Dans sa version simplifiée, le perceptron est monocouche et n'a qu'une seule sortie (booléenne) à laquelle toutes les entrées (booléennes) sont connectées. Plus généralement, les entrées peuvent être des nombres réels.

Mark1, le premier perceptron du monde
Mark1, le premier perceptron du monde

Structure d'un perceptron

Voici comment un neurone est schématiquement représenté dans le fonctionnement du cerveau humain.

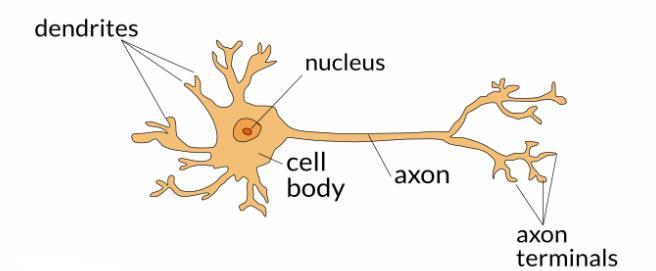
Neurone humain
Neurone humain

Un perceptron est une modélisation mathématique du fonctionnement d’un vrai neurone biologique et qui imite grossièrement le fonctionnement de ce dernier. Il reçoit en paramètre des entrées X dont chaque entrée est multipliée par un poids w. Toutes ces entrées sont alors sommées et passé dans une fonction dite d’activation ou fonction de transfert. Cette fonction va comparer la somme pondérée à un à un certain seuil b pour décider quel sera la sortie y du neurone.

Structure d'un neurone artificiel
Structure d’un neurone artificiel avec n entrées xi et une sortie y

Comme nous pouvons le constater, sa structure est composée de 6 parties :

  • Les entrées ($x_1, x_2, x_3, ..., x_n$)
  • Les poids ($w_1, w_2, w_3, ..., w_n$)
  • Une fonction somme ($\sum$)
  • Un biais ($w_0$)
  • Une fonction d'activation ($h$ qu'on note souvent par la notation grec $\phi$)
  • Une sortie ($y$)

Sur la précédente figure, les entrées sont les données que l’on fournit au perceptron afin qu’il calcule un résultat. Ces données doivent être des mesures en lien avec le cas étudié. Dans le cadre de ce travail, les mesures sont des pixels. Étant donné que les données utilisées peuvent varier, on peut avoir certains problèmes de confiance avec les résultats obtenus

En effet, si nous imaginons qu’une entrée peut avoir des valeurs qui varient entre 0 et 1 et qu’une deuxième entrée peut avoir des valeurs qui varient entre 0 et 3000, alors la deuxième entrée va avoir un impact beaucoup plus important dans le résultat calculé. Afin de remédier à cela, il est impératif de normaliser les données en entrée. Nous verrons plus tard que la normalisation peut avoir un impact sur l’apprentissage.

La fonction de somme pondérée va faire la somme de la multiplication de chaque entrée par son poids correspondant et va ajouter le biais, qui est une valeur constante. Avant de pouvoir utiliser le résultat, la somme est passée dans une fonction d’activation.

  • La fonction Sigmoïde : Pour une valeur $\boldsymbol{x}$ quelconque, $\boldsymbol{y}$ reste entre 0 et 1. Ce cas est très utile lorsque nous avons besoin d’avoir un résultat continu. Elle est généralement notée par le symbole grec $\boldsymbol{\sigma}$ représentée par la fonction $\boldsymbol{\sigma(x) = \frac{1}{e^{-x}}} $.
  • La fonction $\boldsymbol{tanh}$ est également appelée tangente hyperbolique : Cette fonction ressemble à la fonction Sigmoïde. La différence avec la fonction Sigmoïde est que la fonction $tanh$ produit un résultat compris entre $\boldsymbol{-1}$ et $\boldsymbol{1}$.
  • La fonction ReLU (Unité linéaire rectifiée) : Cette fonction converge plus rapidement, optimise et produit la valeur souhaitée plus rapidement. C’est de loin la fonction d’activation la plus populaire utilisée dans les couches cachées sur un réseau de neurones. La fonction $ReLU$ est interprétée par la formule : $\boldsymbol{f(x) = max(0,x)}$.
  • La fonction Softmax : utilisé dans la couche de sortie, sur un réseau de neurones, car il réduit les dimensions et peut représenter une distribution catégorique.

(Vous trouverez encore plus d’autres fonctions sur Wikipédia)

La propagation d’un vecteur d’entrée ($x_i$) à travers un perceptron s’écrit : $$\boldsymbol{p = \sum^{n}_{i=0} x_i w_i - b}$$ (Avec $n$ le nombre d'entrées sur le perceptron) $$\boldsymbol{y = \sigma(p)}$$

Cela dit, un seul neurone ne suffit pas à faire des relations plus complexes. Les neurones on peut en associer plein ensemble, les empiler pour créer des couches de neurones pour réussir à faire des fonctions beaucoup plus compliquées. Et c’est cet ensemble de couche de neurones liées qu’on appelle un "Réseau de neurones" (ou plutôt dire réseau de neurones artificiel).

Apprentissage

Mode d'apprentissage

L’apprentissage d’une MLP peut être faite de plusieurs façons. On trouve l’apprentissage supervisé, non supervisé, par renforcement, semi-supervisé.

Ici sera seulement explicité le mode d’apprentissage supervisé. Ce qui veut dire que les données d’entraînement que vous fournissez à l’algorithme comportent les solutions désirées, appelées étiquettes (en anglais, labels).

Mode d’apprentissage
Un jeu d’entraînement étiqueté pour un apprentissage supervisé (ex. classification de spam)[A. Géron, Hands-On]

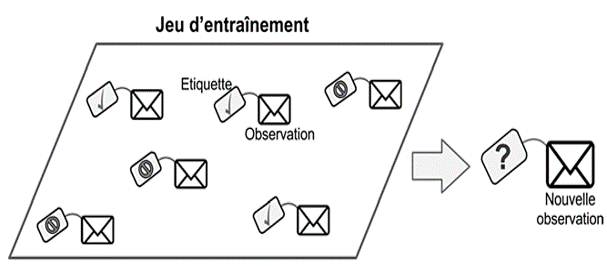
Apprentissage d'un perceptron

Contexte

L’apprentissage consiste à envoyer des données au perceptron et à analyser le résultat. Ensuite, on indique au perceptron quel était le résultat attendu.
Par exemple, si on obtient la valeur $0.3$ mais que la valeur attendue était de $1$, alors l’algorithme d’apprentissage du perceptron détecte qu’il a fait une erreur de $1–0.3=0.7$. Cette valeur peut être vue comme une fonction de coût et le perceptron doit s’adapter (s’ajuster) afin de réduire le coût au minimum possible.

Dans un perceptron nous avons deux types de sortie :

  • Une sortie réelle
  • Une sortie attendue

Si la sortie réelle est différente de la sortie attendue on va soit incrémenter, soit décrémenter le biais afin d'adapter un vecteur de pondération (la somme pondérée)

Pour cela, nous utilisons un algorithme appelé rétropropagation du gradient qui a pour but de changer les poids de chaque connexion. Par ailleur, un poids ou poids synaptique est un coefficient numérique qui est attribué à chacune des entrées d’un neurone, de manière aléatoire au début puis les poids sont adaptés au fur et à mesure, et qui permet de pondérer celles-ci. (Wikipédia, 2017).

Renvoie de l'erreur vers l'arrière
Renvoie de l'erreur vers l'arrière

Si toutes les entrées sont à 0, alors peu importe la valeur des poids donnés à chaque connexion, la valeur en sortie sera toujours 0. Dans ce cas, nous pouvons ajouter le biais qui nous permet de modifier la sortie afin que l’apprentissage se fasse correctement.

Ainsi, l'apprentissage d'un perceptron consiste à envoyer des données et leurs étiquettes sur le perceptron. A la fin, le perceptron doit réussir à trouver les bonnes configurations qui permettent de données une sortie qui se rapproche au sortie voulue. On aura alors une fonction d'erreur qui va calculer l'erreur faite par le perceptron, et cet erreur sera envoyée vers l'arrière pour corriger le poids ET/OU le biais pour que la sortie du perceptron se rapproche le plus proche possible du sortie désirée la rétropropagation (du gradient) ou en anglais Backpropagation.
Ce qu'on peut résumer par : Le perceptron évolue en apprenant de ces erreurs (essaie - erreurs).

Le biais

Pour une bonne compréhension de ce qu’est le biais, nous allons considérer la fonction linéaire $\boldsymbol{y=ax}$. Et nous allons essayer de séparer deux ensembles de données (ici bleu et rouge).

Séparation de deux ens title=
Séparation de deux ensembles

Et comme nous pouvons le constater, la fonction $y=ax$ sépare parfaitement les deux ensembles.

Séparation de deux ensembles à l'aide d'une fonction linéaire
Séparation de deux ensembles à l'aide d'une fonction linéaire

Cependant, la limitation de ces fonctions se présente lorsque les ensembles de données sont moins faciles à séparer.
Sur la figure suivante, on remarque qu’aucune fonction ne permet de séparer les ensembles correctement avec une fonction linéaire. C’est de cette façon qu’on introduit le biais.

Séparation impossible à l'aide une fonction linéaire
Séparation impossible à l'aide une fonction linéaire

Le biais va permettre de rendre la séparations d'ensembles facile en permettant de mieux ajuster les limites entres les ensembles. Elle permet, en effet, d'avoir la possibilité de déplacer les droites séparateurs sur les axes. Dans ce cas, on a pas forcement une droite qui passe par l'origine. Et c'est effet qui va permettre de trouver les limites entres les ensembles.

Sur la figure suivante, la fonction utilisée est $\boldsymbol{y = ax + b}$ (une fonction affine) où $\boldsymbol{+b}$ correspond au biais. Grâce à ce biais, nous avons pu trouver la bonne droite $\boldsymbol{y=−0.3+9}$ : une fonction affine qui sépare bien les ensembles.

Séparation de deux ensemble à l'aide d'une fonction affine
Séparation de deux ensemble à l'aide d'une fonction affine

Le problème XOR

Le perceptron comme nous l'avons vu peut prendre plusieurs éléments en entrées et produire un résultat en sortie. Les éléments d'entrées peuvent être de tout type. Jusque-là, un un perceptron accepte plusieurs types d'entrées et produit de bons résultats.

Et pourtant, on peut tomber sur des ensembles dont leur distributions n'est pas facile à séparer en utilisant un seul forme géometrique en l'occurence une droite.

Prenons cet exemple:

On a vu qu'en utilisant le biais, nous pouvons déplacer un droite (ou tout autre forme géométrique) librement sur les axes d'un repère pour trouver la limites entres des ensembles de donées.

Recapitulatif Biais
Deux ensembles séparé par une droite affine

Supposons maintenant que nous avons des ensembles qui se distribuent de la façon suivante :

Séparation impossible avec une seule droite
Séparation impossible avec une seule droite

On peut voir qu'une seule droite ne permet de les séparer correctement. Il en faudra deux pour le faire.

Séparation avec deux droites
Séparation d'ensembles avec deux droites

Il faut savoir ici qu'une droite représente un perceptron et le fait d'avoir utilisé deux montre qu'un seul perceptron ne peut pas résoudre des problèmes complexes. Il en faudra regrouper plusieurs pour résoudre des problèmes qui se répartissent d'une manière qu'on ne peut pas les découper avec un seul.

Le fait de regrouper les perceptrons pour résoudre une tâche constitue un réseaux de neurones ( Perceptron monocouche ou perceptron multicouche)

On peut alors comprendre ici qu'un seul neurone ne suffit pas de faire des relations plus complexes. Les neurones on peut en associer plein ensemble, les empiler pour créer des couches de neurones pour réussir à faire des fonctions beaucoup plus compliquées. Et c’est cet ensemble de couche de neurones liées qu’on appelle un réseau de neurones (ou plutôt dire réseau de neurones artificiel).

Réseaux de neurones

Réseau de neurones monocouche

Le réseau le plus simple est Le perceptron monocouche.

  • Il possède $N$ informations en entrées.
  • Il est composé de $p$ neurones, que l’on représente généralement alignés verticalement ou horizontalement.
  • Chacun des $p$ neurones est connecté aux $N$ informations d’entrées.
  • La sortie de chacun des $p$ neurones est une est une sortie du réseau.

Une utilisation courante est que chaque neurone de la couche représente une classe. Pour un exemple $X$ donné, on obtient la classe de cet exemple en prenant la plus grande des $p$ sorties

Réseau de neurones monocouche
Réseau de neurones monocouche

Réseau de neurones multicouche

Dans un réseau réseau de neurones multicouche (MLP pour Multi Layer Perceptron), les neurones de la première couche reçoivent toutes les informations entrées, ceux de la deuxième reçoivent toutes les sorties des neurones de la première couche, et ainsi de suite jusqu’aux neurones de la dernière couche.

Réseau de neurones multicouche
Réseau de neurones multicouche

Pour créer un tel réseau, il faut connecter un ensemble de neurones (une couche de neurones) avec un autre ensemble de neurones. Habituellement, chaque neurone d'une couche est connecté à tous les neurones de la couche suivante et celle-ci seulement. Ceci nous permet d'introduire la notion de sens de parcours de l'information (de l'activation) au sein d'un réseau et donc de définir les concepts de neurones d'entrée et neurones de sortie. Par extension, on appelle couche d'entrée l'ensemble des neurones d'entrée(input layer), couche de sortie l'ensemble des neurones de sortie (output layer). Les couches intermédiaires n'ayant aucun contact avec l'extérieur sont appelés couches cachées (hidden layer).

Dans la figure suivante, on voit que chaque neurone d’une couche est lié avec tous les neurones de la couche suivante. Un tel réseau de neurone est appelé réseau complètement connecté (fully connected network en Anglais).

Réseau de neurones multicouche
Réseau de neurones multicouche

Fonctionnement d'un réseau de neurones

Le principe de fonctionnement d’un perceptron et d’un réseau de neurones multicouche est essentiellement le même : nous avons toujours des entrées et des sorties mais nous avons des couches intermédiaires appelées couches cachées. Pour finir, chaque neurone contient aussi une fonction de somme, une fonction d’activation et un biais.

Apprentissage d'un réseau de neurones

Le principe d'apprentissage d'un résau de neurones est le même que celle que nous avons vu dans la section Apprentissage d'un perceptron . La différence est que sur un réseau de neurones l'erreur est envoyé vers tous les neurones de chaque couche et de cette façon, le réseau se réajuste et trouve les bonnes configurations à adopter.

La Rétropropagation (du gradient)

La Rétropropagation (Backpropagation en anglais) est un raccourci pour la propagation d'erreur vers l’arrière , car une erreur est calculée à la sortie et est distribuée vers l’arrière à travers les couches du réseau. On souhaite trouver un minimum global pour une fonction de coût, tout en évitant les éventuelles vallées et minimum locaux qui nous empêcherait de converger vers la solution la plus optimisé pour notre réseau de neurones. Cette rétropropagation du gradient va se faire via l’alternation successives entre deux phases : phase avant et phase arrière.

Phase avant

C’est la phase de prédiction. On envoi à notre réseau une donnée et il va essayer d’en prédire un résultat (par exemple la classe de sortie). Il va avoir un échange d’informations, de valeurs et de sommes, entre chaque neurone et chaque couche. Les données transitent de la couche d’entrée vers la couche de sortie.

Propagation de l’information vers l’avant
Phase avant : Propagation de l’information vers l’avant

Phase arrière

C’est la phase d’apprentissage. En effet, L'erreur est propagée vers l'arrière jusqu'à la couche précédente. À la suite du passage d’une donnée au sein du réseau, nous allons avoir un résultat concernant la prédiction. Les poids et biais du réseau sont initialisé de façon aléatoire, et vont être mis à jour au fil des entraînements via ce procédé.

Propagation de l’information vers l’avant
Phase avant : Propagation de l’information vers l’avant

Fonction de coût

Une fonction de coût communément appelée fonction de perte ou fonction objective (loss function) est une méthode qui sert à évaluer dans quelle mesure un modèle spécifique modélise les données.

On peut citer par exemple :

  • Mean Squared Error (MSE) : Erreur quadratique moyenne généralement utilisé dans les problème de régression (le dernier couche contiendra un nœud avec une fonction d’activation linéaire),
  • Cross-Entropy : (entropie croisée) également appelée perte logarithmique utilisé dans les problèmes de classification binaire (Le dernier couche contiendra un neurone avec sigmoïde comme fonction d’activation),
  • Cross-Entropy : pour une classification multi-classe. Le dernier couche contiendra un nombre de neurones correspondant au nombre de classe et chacun aura comme fonction d’activation Softmax.

La descente du gradient

La Descente du Gradient est un algorithme d’optimisation qui permet de trouver le minimum de n’importe quelle fonction convexe en convergeant progressivement vers ce minimum. Cette descente peut s’effectuer soit de manière globale (batch gradient), soit par des lots (mini batch gradient), soit de façonunitaire (stochastic gradient). La première consiste à envoyer au réseau la totalité des données d’un seul trait, et de faire ensuite le calcul du gradient ainsi que la correction des coefficients. Alors que la seconde consiste à envoyer au réseau, les données par petit groupe d’une taille définit par l’utilisateur. La dernière quant à elle, envoi une donnée à la fois dans le réseau.

Dans notre cas, le réseau qu’on va créer utilisera la méthode par mini batch. En effet, celle-ci permet une meilleure convergence par rapport à la stochastic, et nous permet de meilleures performances que la batch gradient, car on ne charge pas entièrement nos données.

Descente de gradient
Descente de gradient

Minimisation de la fonction de coût

Dans les réseaux de neurones, on utilise l’algorithme de la Descente de Gradient dans les problèmes d’apprentissage supervisé pour minimiser la fonction coût, qui, justement, est une fonction convexe comme le montre la figure suivante. Les algorithmes d’optimisation (à savoir Adam, RAdam, SGD, RMSprop, etc.) utilisent un hyperparamètre nommé learning rate (en français Taux d’apprentissage) pour converger vers le minimum de cette fonction.

Si le Learning Rate est trop grand, alors vous ferez de trop grands pas dans la descente de gradient. Cela a l’avantage de descendre rapidement vers le minimum de la fonction coût, mais vous risquez de louper ce minimum en oscillant autour à l’infini… ( Guillaume 2019)

Pour éviter le cas précédent, vous pourriez être tenté de choisir un Learning Rate très faible. Mais s’il est trop faible, alors vous risquez de mettre un temps infini avant de converger vers le minimum de la fonction cout. ( Guillaume 2019)

Minimisation de l'erreur par descente de gradient
Minimisation de l'erreur par descente de gradient

L'algorithme de descente de gradient utilisé pour entraîner le réseau (i.e. mettre à jour les poids) est donné par : $\boldsymbol{{w'}_i=w_i - {\eta{.}\frac{dE}{dw_i}}}$

Où :

  • $\boldsymbol{w_i}$ : Est la valeur des poids avant mise à jour
  • $\boldsymbol{{w'}_i}$ : Est la valeur des poids après mise à jour
  • $\boldsymbol{\eta}$ : Est le taux d'apprentissage (learning rate)

Conclusion

Les principaux éléments à retenir sont les suivants :

  • Un réseau de neurones est un système composé de neurones, généralement répartis en plusieurs couches connectées entre elles.
  • Un tel système s'utilise pour résoudre divers problèmes statistiques, mais nous nous intéressons ici qu'au problème de classification (très courant). Dans ce cas, le réseau calcule à partir de l'entrée un score (ou probabilité) pour chaque classe. La classe attribuée à l'objet en entrée correspond à celle de score le plus élevé
  • Chaque couche reçoit en entrée des données et les renvoie transformées. Pour cela, elle calcule une combinaison linéaire puis applique éventuellement une fonction non-linéaire, appelée fonction d'activation. Les coefficients de la combinaison linéaire définissent les paramètres (ou poids) de la couche
  • Un réseau de neurones est construit en empilant les couches : la sortie d'une couche correspond à l'entrée de la suivante.
  • Cet empilement de couches définit la sortie finale du réseau comme le résultat d'une fonction différentiable de l'entrée
  • La dernière couche calcule les probabilités finales en utilisant pour fonction d'activation la fonction logistique (classification binaire) ou la fonction Softmax (classification multi-classes)
  • Une fonction de perte (loss function) est associée à la couche finale pour calculer l'erreur de classification. Il s'agit en général de l'entropie croisée (cross entropy).
  • Les valeurs des poids des couches sont apprises par rétropropagation du gradient : on calcule progressivement (pour chaque couche, en partant de la fin du réseau) les paramètres qui minimisent la fonction de perte régularisée. L'optimisation se fait avec une descente du gradient.