Les réseaux de neurones convolutionnels
Introduction
Les réseaux de neurones convolutifs (CNN), sont, jusqu’à maintenantMaintenant : 2020 , les meilleurs modèles de réseaux de neurones pour classifier des images. Elles prennent en entrée une image fournie sous la forme d’une matrice de pixels. Cette matrice est de deux dimensions pour une image en niveau de gris. La couleur est représentée par une troisième dimension, de profondeur 3 pour représenter les couleurs fondamentales [Rouge, Vert, Bleu} (RGB de l'anglais Red, Green, Blue).
Avant de continuer, rappelons-nous qu’un CNN est avant tout un réseau de neurone que l’on a juste
ajouté un ou plusieurs couches de convolutions. Donc, les CNN respectent aussi les règles d’un
réseau de neurones cités sur cette
section du chapitre
Les réseaux de neurones
.
Les réseaux de neurones convolutifs, ou CNN, ont été conçus pour mapper les données d'image à une variable de sortie. Ils se sont révélés si efficaces qu'ils sont la méthode de référence pour tout type de problème de prédiction impliquant des données d'image en entrée. L'avantage d'utiliser des CNN est leur capacité à développer une représentation interne d'une image bidimensionnelle. Cela permet au modèle d'apprendre la position et l'échelle dans différentes structures des données, ce qui est important lorsque vous travaillez avec des images.
L'avantage de CNN est que :
- Ils utilisent moins de paramètres (poids) pour apprendre qu'un réseau entièrement connecté.
- Ils sont conçus pour être invariants à la position et à la distorsion de l'objet dans l’image.
- Ils apprennent et généralisent automatiquement les fonctionnalités du domaine d'entrée.
Architecture de réseaux de neurone convolutionnel
Il existe trois types de couches dans un réseau neuronal convolutif :
Couche de convolution
Les couches convolutives sont composées de filtres et de carte de caractéristiques. Son but est de repérer la présence d'un ensemble de caractéristiques dans les images reçues en entrée.
Les filtres sont les neurones
de la couche. Ils ont des poids d'entrée et produisent une valeur. La
taille d'entrée est un carré fixe appelé
patch
ou
champ récepteur
.
Si la couche convolutionnels est une
couche d'entrée, alors le patch d'entrée sera des valeurs de pixels. Si la couche est interne
(cachée), alors la
couche convolution prendra l'entrée d'une carte de caractéristique de la couche précédente.
La couche de convolution reçoit donc en entrée plusieurs images, et calcule la convolution de
chacune
d'entre elles avec chaque filtre. On obtient pour chaque paire (image, filtre)
une carte d'activation
, ou
feature map
,
qui nous indique où se situent les features dans l'image : plus
la valeur est élevée, plus
l'endroit correspondant dans l'image ressemble à la feature.
Contrairement aux méthodes traditionnelles, les features ne sont pas prédéfinies selon un formalisme particulier (par exemple SIFT), mais apprises par le réseau lors la phase d'entraînement ! Les noyaux des filtres désignent les poids de la couche de convolution. Ils sont initialisés puis mis à jour par rétropropagation du gradient.
Qu'est-ce qu'une convolution ?
Une convolution est un filtre qui passe sur une image, la traite et extrait des
caractéristiques qui
montrent une similitude dans l'image. Un filtre est tout simplement un ensemble d’une
matrice qu’on
appelle aussi noyau de convolution ou filtre. Ce filtre on l’applique sur un voisinage d’une
image et en
sortie on aura une image résultante différente de l’original qu’on appelle features map
.

Appliquer donc une convolution consiste à sélectionner un pixel $\boldsymbol{𝒊}$ sur une image, le multiplier par le multiplicateur sur le filtre lui correspondant, et faire de même sur chacun de ses voisins. Enfin la nouvelle valeur du pixel $\boldsymbol{i}$ est la somme de tous ces résultats. La fonction d’activation ReLU remplace donc toutes les valeurs négatives reçues en entrées par des zéros. Cela peut sembler étrange mais voici certains résultats :
Couche de convolution
En plus d'utiliser des convolutions, la mise en commun nous aide grandement à détecter les fonctionnalités. L'objectif est de réduire la quantité globale d'informations dans une image, tout en conservant les fonctionnalités détectées comme présentes. Une couche de Pooling est souvent placée entre deux couches de convolution : elle reçoit en entrée plusieurs feature maps, et applique à chacune d'entre elles l'opération de pooling. L'opération de pooling consiste à réduire la taille des images, tout en préservant leurs caractéristiques importantes.
Pour cela, on découpe l'image en cellules régulière, puis on garde au sein de chaque cellule la valeur maximale. En pratique, on utilise souvent des cellules carrées de petite taille pour ne pas perdre trop d'informations. Les choix les plus communs sont des cellules adjacentes de taille 2 × 2 pixels qui ne se chevauchent pas, ou des cellules de taille 3 × 3 pixels, distantes les unes des autres d'un pas de 2 pixels (qui se chevauchent donc). On obtient en sortie le même nombre de feature maps qu'en entrée, mais celles- ci sont bien plus petites.
Il existe différents types de Pooling, mais dans notre travail, nous en utiliserons un appelé Max Pooling (Pooling maximal).
L'idée ici est d'itérer sur l'image et de regarder le pixel et ses voisins immédiats à droite, en dessous et à droite en dessous. Prenez le plus grand (d'où le nom MAX pooling) d'entre eux et chargez-le dans la nouvelle image. Ainsi, la nouvelle image sera 1/4 de la taille de l'ancienne - les dimensions sur X et Y étant divisées par deux par ce processus. Les caractéristiques sont maintenues malgré cette compression.
Couches entièrement connectées (fully-connected)
La couche fully-connected constitue toujours la dernière couche d'un réseau de neurones,
convolutif ou non elle n'est donc pas caractéristique d'un CNN. La dernière couche
fully-connected
permet
de classifier l'image en entrée du réseau : elle renvoie un vecteur de taille
$\boldsymbol{N}$,
où $\boldsymbol{N}$ est le nombre de classes dans notre problème de classification d'images.
Chaque élément du vecteur indique la
probabilité pour l'image en entrée d'appartenir à
une classe.
En résumé
Le réseau de neurones convolutif apprend les valeurs des poids de la même manière qu'il apprend les filtres de la couche de convolution : lors de phase d'entraînement, par rétropropagation du gradient. La couche fully-connected détermine le lien entre la position des features dans l'image et une classe.

Choix des paramètres
Un réseau de neurones convolutif se distingue d'un autre par la façon dont les couches sont empilées, mais également paramétrées. Les couches de convolution et de pooling possèdent en effet des hyperparamètres, c'est-à-dire des paramètres dont vous devez préalablement définir la valeur. Les CNN utilisent plus de paramètres qu'un MLP standard. Même si les règles habituelles pour les taux d'apprentissage et des constantes de régularisation s'appliquent toujours, il faut prendre en considération les notions de nombre de filtres, leur forme et la forme du max pooling.
Les features de la couche de convolution et les poids de la couche fully-connected ne sont pas des hyperparamètres, puisqu'ils sont appris par le réseau de neurones lors de la phase d’entraînement !
La taille des feature maps en sortie des couches de convolution et de pooling dépend des hyperparamètres. Chaque image (ou feature map) est de dimensions $lxhxd$, où $l$ est sa largeur en pixels, $h$ sa hauteur en pixels et $d$ le nombre de canaux ($1$ pour une image en noir et blanc, $3$ pour une image en couleurs).
La couche de convolution
La couche de convolution possède quatre hyperparamètres :
- Le nombre de filtres $\boldsymbol{k}$
- La taille $\boldsymbol{f}$ des filtres : chaque filtre est de dimensions $\boldsymbol{f × f × d}$ pixels.
- Le pas $\boldsymbol{s}$ avec lequel on fait glisser la fenêtre correspondant au filtre sur l'image. Par exemple, un pas de $\boldsymbol{1}$ signifie qu'on déplace la fenêtre d'un pixel à la fois.
- Le zero-padding $\boldsymbol{p}$ : on ajoute à l'image en entrée de la couche un contour noir d'épaisseur $\boldsymbol{p}$ pixels. Sans ce contour, les dimensions en sortie sont plus petites. Ainsi, plus on empile de couches de convolution avec $\boldsymbol{p = 0}$ , plus l'image en entrée du réseau rétrécit. On perd donc beaucoup d'informations rapidement, ce qui rend la tâche d'extraction de features difficile.
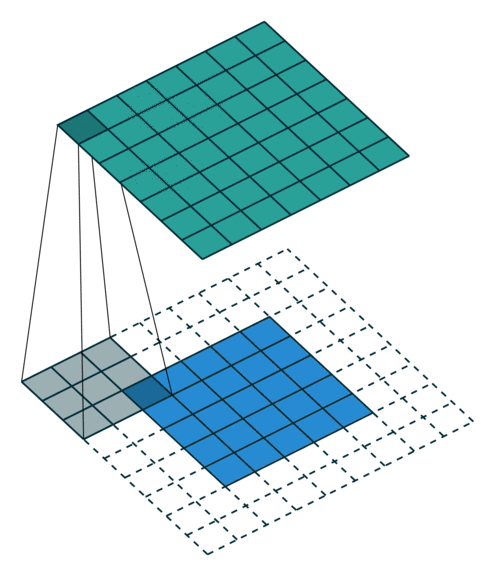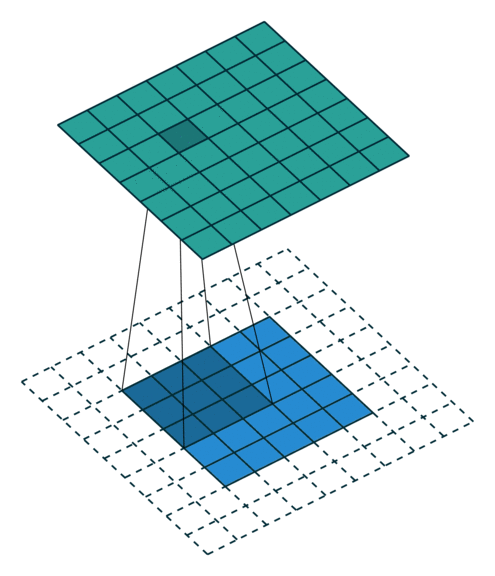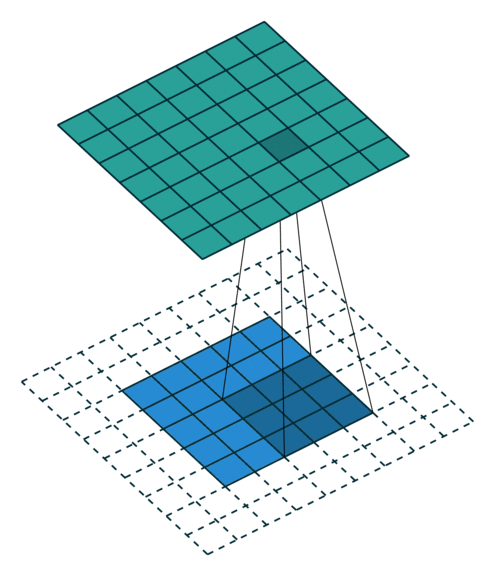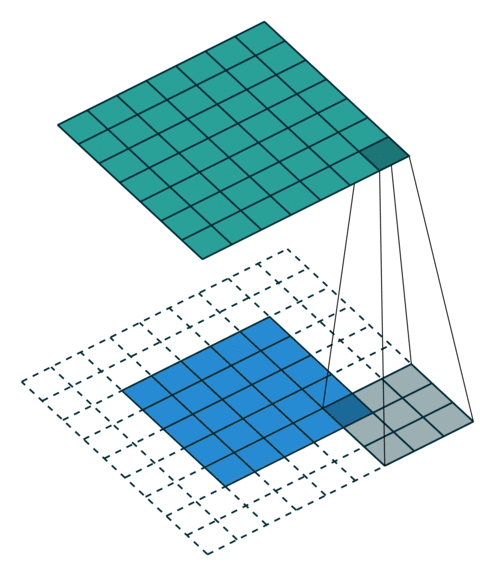
La couche de pooling
La couche de pooling présente seulement deux hyperparamètres :
- La taille $\boldsymbol{f}$ des cellules : l'image est découpée en cellules carrées de taille $\boldsymbol{f × f}$ pixels
- Le pas $\boldsymbol{s}$ : les cellules sont séparées les unes des autres de $\boldsymbol{s} pixels$
Methodes de régularisation
Pour ne pas tomber dans le problème de sur apprentissage il y a des méthodes de régularisation à utiliser.
Empirique
Dropout
Les couches "FC" (Fully Connected) occupent la majeure partie de la mémoire du CNN. D'ailleurs le concept de FC crée un problème exponentiel de mémoire appelé "Overfitting" ("sur-connexion" conduisant au sur-apprentissage) ralentissant le traitement de l'information. Pour prévenir cela, la méthode du dropout est utilisée pour "éteindre" les neurones aléatoirement (avec une probabilité prédéfinie, souvent un neurone sur deux) ainsi que les neurones périphériques. Ainsi, avec moins de neurones, le réseau est plus réactif et peut donc apprendre plus rapidement. À la fin de la séance d'apprentissage, les neurones "éteints" sont "rallumés" (avec leurs poids originaux). Plus la couche FC est proche de l'image source, moins on éteindra de neurones. L'objectif est d'éteindre et rallumer les neurones aléatoirement, dans le cadre d'entraînements successifs. Une fois les séries d'entraînements terminées, on rallume tous les neurones et on utilise le réseau comme d'habitude. Cette technique a montré non seulement un gain dans la vitesse d'apprentissage, mais en déconnectant les neurones, on a aussi limité des effets marginaux, rendant le réseau plus robuste et capable de mieux généraliser les concepts appris.
DropConnect
Le DropConnect est une évolution du dropout, où on ne va non plus éteindre un neurone, mais une connexion (l'équivalent de la synapse), et ce de manière toujours aléatoire. Les résultats sont similaires (rapidité, capacité de généralisation de l'apprentissage), mais présentent une différence au niveau de l'évolution des poids des connexions. Une couche FC avec un DropConnect peut s'apparenter à une couche à connexion "diffuse".
- La régularisation par norme 1 : La spécificité de cette régulation est de diminuer le poids des entrées aléatoires et faibles et d'augmenter le poids des entrées "importantes". Le système devient moins sensible au bruit.
- La régularisation par norme 2 : (norme euclidienne) La spécificité de cette régulation est de diminuer le poids des entrées fortes, et de forcer le neurone à plus prendre en compte les entrées de poids faible.
Les régularisations par norme 1 et norme 2 peuvent être combinées : c'est la "régularisation de réseau élastique" (Elastic net regulation).
Explicite
Taille du réseau
La manière la plus simple de limiter le sur apprentissage est de limiter le nombre de couches du réseau et de libérer les paramètres libres (connexions) du réseau. Ceci réduit directement la puissance et le potentiel prédictif du réseau. C'est équivalent à avoir une "norme zéro".
Dégradation du poids
Le concept est de considérer le vecteur des poids d'un neurone (liste des poids associés aux signaux entrants), et de lui rajouter un vecteur d'erreur proportionnel à la somme des poids (norme 1) ou du carré des poids (norme 2 ou euclidienne). Ce vecteur d'erreur peut ensuite être multiplié par un coefficient de proportionnalité que l'on va augmenter pour pénaliser davantage les vecteurs de poids forts.
Conclusion
Dans ce chapitre nous avons évoqué les réseaux de neurones du type Feed-forward aussi connu sous le nom de Réseau de type perceptron. Ainsi, nous nous sommes un peu attardés sur les perceptrons multicouches qui comporte des neurones complètement connectés. Nous avons aussi parler de réseaux neuronal convolutifs. Ces réseaux sont capables d’extraire des caractéristiques d’images présentées en entrée et de classifier ces caractéristiques. Le succès des CNN ces dernières années dépend principalement des trois piliers suivants : données, modèle et puissance de calcul.
Les réseaux de neurones convolutionnels présentent cependant un certain nombre de limitations, en premier lieu, les hyper paramètres du réseau sont difficiles à évaluer a priori. En effet, le nombre de couches, les nombre de neurones par couche ou encore les différentes connexions entre couches sont des éléments cruciaux et essentiellement déterminés par une bonne intuition ou par une succession de tests/calcul d’erreurs (ce qui est coûteux en temps). Le nombre d’échantillons d’apprentissage est également un élément déterminant, et il arrive souvent que celui–ci soit trop faible en comparaison du nombre de paramètres (poids) du réseau. Des solutions existent comme augmenter artificiellement leur nombre ou encore en réduisant le nombre de paramètres libres (en réalisant un préapprentissage des premières couches par exemple).
Dans le prochain chapitre, nous allons mettre en pratique les CNN avec l’implémentation de notre propre modèle de deep learning.






